There is a new craze lately about a simple game named Wordle.  The idea is somewhat similar to the old game of Mastermind:

1. There is a hidden five-letter word you try to guess.
2. For each guess, you get feedback if a specific letter is: (a) correct and in the correct location (b) correct but in the wrong location or (c) not correct and not from another location.
3. You have a total of six guesses to try the word.

A new Wordle is released each day.  Just in the last few weeks, I heard a lot more about this game – and also tried its web site on recent.

One of the posts on Facebook I had from a friend was asking for feedback on strategies people use for solving the same.  This led me to explore a bit more and also go down the path to think about  what might be involved in optimal guesses and whether I could create a solver for this.  This posting describes a four step build-up I consider for creating such a solver.  Some of these steps I’ve also done.

As I looked more, I also found some resources including how others have solved the same problem.  Rather than look in detail at their solutions – I decided I’d rather explore that first on my own.  However, I did get references to a few useful resources I can use for my construction (these coming from responses to that original Facebook post including links they made):

• There is a Google corpus of words they found most common on the internet: https://www.kaggle.com/rtatman/english-word-frequency .  This contains 39,933 total five letter words.  That is more than those that would be accepted as valid guesses, but also useful in creating an algorithm that is more robust.
• There are pointers to the list of 12972 words you are allowed to guess: https://docs.google.com/spreadsheets/d/1KR5lsyI60J1Ek6YgJRU2hKsk4iAOWvlPLUWjAZ6m8sg/edit#gid=0 as well as the 2315 actual words that can be in the solution: https://docs.google.com/spreadsheets/d/1-M0RIVVZqbeh0mZacdAsJyBrLuEmhKUhNaVAI-7pr2Y/edit#gid=0  It seems to me the actual mystery list of answers seems a bit like cheating, but willing to consider using the guessable list to find acceptable candidates.  However, focus first on creating something from the larger Google word list. 
• There is an interesting variant to Wordle that keeps changing the word to make it maximally hard – https://www.pcgamer.com/absurdle-is-like-wordle-but-it-fights-back/  This Absurdle program seems like a good test proxy to make sure my program can find guesses in a minimal amount of guesses.

Using these resources – following are the four steps I’ve considered to creating a solver.

Step #1 – create solver aids

The idea here is to create some utility programs including one that can filter a word list to include only those that match a particular Wordle response.  For example the Wordle response says the second letter is “a” and it is in the correct location, the letter “y” is in the solution but not the first letter and letters “u”, “o” and “d” are not found … then filter the remaining words to match the guess.

I’ve implemented this filter and with it I can use the Google word corpus to help me filter the remaining lists to look for candidates in order of word frequency.  This helps me steadily narrow the list and look at candidates for potentially being the answer.

Note: Even though these are candidates for the actual solution, there could be reasons one might want to use other words as guesses.  The primary reason is if those other guesses might more efficiently rule in/out letters than just matching only for ones you already know.

Step #2 – create something that picks an optimal guess from the (remaining) word list

The idea here is to take a look at a word list, e.g. from the narrowed candidates, and pick a guess that might optimally separate them for further narrowing.

So how to do this? and what is an optimal guess?

My suggestion for this is based on an observation that there are 238 possible valid response codes that Wordle can provide as feedback.  In particular:

• Each of the five letters guessed can have one of three response categories: [a] the guess is a match in the right location [b] the guess is a match but not in this location [c] the guess is not a match.  So 3x3x3x3x3 = 243 possible combinations of these responses.
• Five of those combinations will never occur.  In particular: four of your letters are correct, the fifth is not and is in the wrong location
• 243 – 5 = 238 possible responses

So, we can evaluate each guess based on the effect it has on the candidate list.  We can look at things such as “how many buckets are occupied” and “what is the maximal number of elements in any bucket”.  As an initial implementation, I’ll start with the “minimize the largest bucket” heuristic and see how well it does.

I have implemented such a guesser.  It can serve as basic framework for a solver.  Each round uses the same candidate words as guesses but applies to a steadily narrowing remaining list of candidates.

Note: Using the Google list of words as candidate guesses, I have a risk that Wordle itself doesn’t accept as valid choices.  The obvious answer to this would to instead use the Wordle candidate list – which is what I implemented by default in the prototype.

Step #3 – validate and tune this guessing logic by trying all possible combinations – as well as Absurdle

With a guesser created in step #2, one can evaluate performance for all possible combination of five letter hidden words.  This would be ~40,000 possible iterations of the guesser algorithm – to find the maximal possible chains of guesses.

While exhaustive search might not be the most elegant way of doing such validation, the total combinatorics here seem small enough that it is well in the range of current compute power.

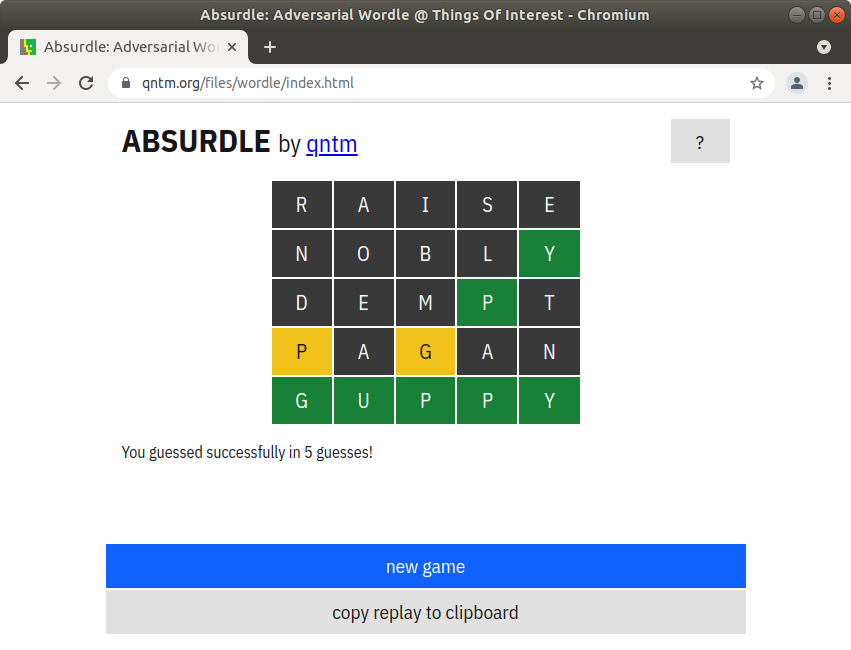
I haven’t yet tried an exhaustive evaluation, but have tried Absurdle.  Following is a rough transcript of the guesses and end result

### Generate a list of mystery words "c0.txt" using five letter words in Google corpus.  ### Find the best candidate

prompt% ./five_letter unigram_freq.csv > c0.txt
prompt% ./guess -m c0.txt | sort -n +2 +3 | more

# Guess 'raise' and Absurdle tells me there are no matches

### Filter out the candidate list based on Absurdle response
prompt% ./filter -i c0.txt -g nobly -c '?????' -p '?????' > c1.txt

### Find the best candidate to narrow the remaining list
prompt% ./guess -m c1.txt | sort -n +2 +3 | more

# Guess 'nobly' and Absurdle tells me the 'y' at the end matches

### Filter out the candidate list based on Absurdle response
prompt% ./filter -i c1.txt -g nobly -c '????y' -p '?????' > c2.txt

# Find the best candidate to narrow the remaining list
prompt% ./guess -m c2.txt | sort -n +2 +3 | more

# Guess 'dempt' and Absurdle tells me the 'p' at 4th position matches

### Filter out the candidate list based on Absurdle response
prompt% ./filter -i c2.txt -g dempt -c '???p?' -p '?????' > c3.txt

### Find the best candidate to narrow the list (or can also guess twice)
prompt% ./guess -m c3.txt | sort -n +2 +3 | more

# Guess 'pagan' and Absurdle tells me the 'p' and 'g' are at wrong positions

### Filter out the candidate list based on Absurdle response
prompt% ./filter -i c3.txt -g pagan -c '?????' -p 'p?g??' > c4.txt

# Guess 'guppy and Absurdle tells me I successfully guessed in five guesses!

Step #4 – automate this to interact with the web page

I will likely never do this step, but the basic idea is to create an actual program that fetches the web page and provides responses.

There presumably are existing building blocks for doing most of this.  I have used one such tool named xdotool to do exactly that for a Linux-based Sudoku web page solver.  So it would be mostly building this out and seeing what falls out of testing.

Overview and thoughts on the exercise

There is more interest in creating a solver than actually using it.  What makes Wordle interesting is as a test of human memory to see what words we recall.  Reducing this to a more mechanical computer search exploits what computers can do well – but otherwise misses the human memory aspect.

The choice of word lists to start with can be important.  In particular the difference between the Google Corpus 39933 words is larger to narrow than if you cheat and choose only from the actual mystery list of 2315 words (somewhat cheating in my mind).

There might be refinements if one considers the specific match letter and not just a more general bucket.  For example, when Wordle tells me I have the third letter correct, I put that together in a single bucket regardless of whether the match is “a”, “b”, “c” or anything else.  Expanding out the cases of those matches would significantly grow the tree from my 238 valid possibilities.  I expect some of this is taken care of when I take steps to filter the remaining possibilities with using the match – but some algorithms like sum of squares might be more accurate taking into account the particular match.  I expect an indirect effect is to further emphasize the largest buckets.

The website 538 lists a challenge to see if you can create an algorithm for guessing in Wordle in three guesses or less and probability of achieving success. https://fivethirtyeight.com/features/when-the-riddler-met-wordle/ Haven’t calculated the probability yet, but here is how I would approach it:

1. Use the guess chooser from step #2 above on only the mystery list and it tells me ‘raise’ has the smallest remaining bucket overall and ‘roate’ has the smallest sum of squares.  Use ‘roate’ as maximally spreading out the distribution.
2. Once Wordle responds at most one bucket is going to have 195 words.  The sum of squares helped me spread this overall.
3. Use the response from Wordle to filter the bucket chosen into just the remaining words.
4. Repeat again for second and subsequent guesses

As far as the probabilities go, I’d have to code up the algorithm to see how quickly it could reach each of the 2315 mystery words – essentially a breadth wise search to see how quickly the tree expands.

The overall code was pretty simple to write, 270 non-commented source lines of C total.

Update: After creating my solution, I looked a bit more at other examples out there including this one: https://github.com/LaurentLessard/wordlesolver  referenced at 538.  My approach seems fairly similar except this author has more fully explored the search strategy tradeoffs.